报告主题：Hypergraphs with arbitrarily small 2-degree Turán density

报 告 人：丁来浩 副教授

报告时间：2025年4月18日（周五）下午2：00-2：50

报告地点：44118太阳成城集团602室

报告摘要: For a k-uniform hypergraph (or simply k-graph) F, the 2-degree Turán density π₂(F) is the supremum over all α such that there exist infinitely many F-free k-graphs H such that every pair of V(H) is contained in at least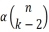 edges. By relating to the vanishing order, which was first introduced by Reiher, Rödl and Schacht in the study of vanishing uniform Turán density, we show that the 2-degree Turán density can be arbitrarily close to zero. This is a joint work with Hong Liu and Haotian Yang.

报告人简介：丁来浩，华中师范大学数学与统计学学院副教授，博士毕业于山东大学，曾前往佐治亚理工学院和韩国基础科学研究院交流访问，主持完成国家自然科学基金青年基金一项。研究方向主要为图染色理论和极值图论, 在Journal of the London Mathematical Society, Journal of Combinatorial Theory-Series B, European Journal of Combinatorics, Discrete Mathematics, Science China-Mathematics 等期刊上发表论文十余篇。

报告主题：How connectivity affects the extremal number of trees

报 告 人：江素云 助理研究员

报告时间：2025年4月18日（周五）下午3：00-3：50

报告地点：44118太阳成城集团602室

报告摘要: The Erdős-Sós conjecture states that the maximum number of edges in an n-vertex graph without a given k-vertex tree is at most n(k-2)/2. Despite significant interest, the conjecture remains unsolved. Recently, Caro, Patkós, and Tuza considered this problem for host graphs that are connected. Settling a problem posed by them, for a k-vertex tree T, we construct n-vertex connected graphs that are T-free with at least (1/4-o_k(1))nk edges, showing that the additional connectivity condition can reduce the maximum size by at most a factor of 2. Furthermore, we show that this is optimal: there is a family of k-vertex brooms T such that the maximum size of an n-vertex connected T-free graph is at most (1/4+o_k(1))nk. This is joint work with Hong Liu and Nika Salia.

报告人简介：江素云，江汉大学人工智能学院助理研究员，2018年博士毕业于山东大学，2016年9月至2017年9月访问佐治亚州立大学，2022年11月至2024年8月访问韩国基础科学研究院，主持完成国家自然科学基金青年基金1项，主持湖北省自然科学基金一般面上1项。研究方向主要包括结构图论和极值图论，在Forum of Mathematics, Sigma, Journal of Combinatorial Theory-Series B, Journal of Graph Theory, Discrete Mathematics等期刊上发表论文十余篇。

报告主题：Forbidden pairs for spanning Θ-subgraphs

报 告 人：王世鹏 讲师

报告时间：2025年4月18日（周五）下午4：10-5：00

报告地点：44118太阳成城集团602室

报告摘要: Let F be a set of connected graphs, and let G be a graph. We say that G is F-free if it does not contain F as an induced subgraph for all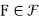, and we call a forbidden pair if 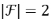. A Θ-graph is the graph consisting of three internally disjoint paths with the same pair of end-vertices. If the Θ- subgraph T contains all vertices of G, then we call T a spanning Θ-subgraph of G. We characterize all  pairs of connected graphs R，S such that every 2-connected {R, S}-free graph has a spanning Θ-subgraph. We also characterize all minimal 2-connected non-cycle claw-free graphs without spanning Θ-subgraphs.

报告人简介：王世鹏，江苏大学讲师，博士毕业于北京理工大学，主要研究方向为结构图论和极值图论。在JCTB, SIAM Discrete Math., JGT, Electroic J. Combin.等期刊发表论文十余篇，主持国家自然科学基金青年基金一项。

初审：王   健

复审：高   犇

终审：杨卫华